Extraocular Muscles and Movements
The vast majority of the test battery for assessing the vestibular system is done indirectly through measuring eye movements. Because so much of vestibular testing relies on the interpretation of eye movements, it is paramount that the vestibular clinician understand how the eyes move, their limitations of motion, eye movement's impact on vision, and potential disorders of the extraocular muscles (EOM). What follows will provide a thorough introduction to these concepts with the aim of increasing your comfort and ability in dealing with eye movements in the clinic.
Anatomy of the Extraocular Muscles1 2 3

FIGURE 1. Source: Wikimedia Commons
There are six muscles (per eye) responsible for generating all movements of the eyes in their bony orbits:
- Lateral Rectus (LR)
- Medial Rectus (MR)
- Superior Rectus (SR)
- Inferior Rectus (IR)
- Superior Oblique (SO)
- Inferior Oblique (IO)
When considered together, with the exception of the inferior oblique, these muscles take on the shape of a cone. They attach to the eye at one end (opening of the cone) and converge upon a tendenous ring called the annulus of Zinn (vertex of the cone). This can be seen in figure 1, along with the inferior oblique's attachment to the nasal portion of the bony orbit.
The superior rectus and superior oblique muscles attach to the top of the eye. The inferior rectus and inferior oblique attach to the bottom of the eye. The lateral rectus and medial rectus attach the sides furthest from and closest to the nose, respectively. Despite the superior oblique belonging to the cone, it takes an indirect route before joining the other EOM at the annulus of Zinn; the SO attaches to the top of the eye, passes through a fibrous ring, called the "trochlea," and then converges with the other EOM (see figure 1).
- Trochlea
- an anatomical structure resembling a pulley: as... the fibrous ring in the inner upper part of the orbit through which the tendon of the superior oblique muscle of the eye passes. 4
The trochlea acts as a pulley for the SO and changes the angle of pull exterted on the eye. This allows the SO to rotate the eye in a manner opposite to the inferior oblique, which, remember, also has a unique angle because it attaches to the nasal portion of the bony orbit instead of at the vertex of the EOM cone.


Movements of the Extraocular Muscles1 2 3
This section might seem a little daunting after reviewing figure 1, but rest assured eye movements involve intuitive mechanics and are actually quite straightforward. In fact, a simple bedside ocular motility test (e.g. part of a standard bedside cranial nerve examination) invokes the six cardinal directions of gaze and therefore tests all six extraocular muscles of both eyes. For those unfamiliar with this test, the patient simply holds the head still and follows the clinician's finger (or other object) as he "draws" a capital "H" in front of the patient (see figure 2).

FIGURE 2.
Yoked Eye Movements
You have just learned the six cardinal directions of gaze from examining figure 2. All of these movements are "yoked," which means EOM in both eyes are working together to move the eyes in the same direction at the same time; what one eye does, the other eye does automatically. For example, if something catches your eye off to the left and your left eye moves quickly to focus the scene, you do not consciously and separately have to tell your right eye to move leftward. Because this direction of gaze ("left") is a yoked eye movement, both eyes respond.
The next step is to delve a little deeper and discuss which extraocular eye muscles are associated with which movements, and what pairs of EOM are yoked together. We'll cover each of the six cardinal directions of gaze, as well as up- and downgaze, and convergence.
» Looking Right (Dextroversion): You already know that the lateral rectus attaches to the side of the eye furthest from the nose. Keeping in mind that muscles can only contract, it makes perfect sense that the LR rotates the eye away from the nose. Thus when looking to the right, the LR of the right eye causes the rightward rotation in the orbit. Eye movement away from the nose is called abduction.
But what about the left eye? The LR of the left eye would rotate the eye to the left, so that is of no use in this case. You learned the medial rectus attaches to the side of the eye closest to the nose, which would pull the left eye to the right side. The MR rotates the eye toward the nose. Movement toward the nose is called adduction. And just like that, you have encountered your first yoked pair of extraocular muscles: the right LR and left MR (see figure 3).

FIGURE 3.
» Looking Left (Levoversion): This gaze requires the same movements as looking to the right, but in the opposite direction. It really is as easy as reversing the EOM we just learned above to achieve leftward gaze: right MR and left LR (see figure 4). In other words, the right eye now needs to move toward the nose, while the left eye needs to move away from the nose.

FIGURE 4.
» Looking Right and Up (Dextroelevation): This direction has a little more nuance to it, but is still easy to comprehend. As seen above, looking right involves the right LR (abduction) and the left MR (adduction). Due to the mechanics of the EOM, when the right eye is fully abducted (away from the nose) it can only be elevated by the superior rectus. Conversely, when the left eye is fully adducted (toward the nose) it can only be elevated by the inferior oblique. Thus we encounter another pair of yoked muscles in looking right and up: the right SR and the left IO (see figure 5).

FIGURE 5.
» Looking Left and Up (Levoelevation): Just as with gaze right vs. left, looking right and up vs. looking left and up involves the same principles and muscles, but applyed to the opposite eyes. That means the left eye is now abducted (away from the nose), so can only be elevate with the SR. The right eye is now adducted (toward the nose), so it can only be elevated by the IO. This yoked pair of muscles is: the right IO and the left SR (see figure 6).

FIGURE 6.
» Looking Right and Down (Dextrodepression): Looking right and down still involves the right LR (abduction) and the left MR (adduction) - that much is the same in this direction of gaze. Similar but new, due to the mechanics of the EOM, when the right eye is fully abducted (away from the nose) it can only be depressed by the inferior rectus. Conversely, when the left eye is fully adducted (toward the nose) it can only be depressed by the superior oblique. Therefore, looking right and down invokes the following yoked muscles: the right IR and the left SO (see figure 7).

FIGURE 7.
» Looking Left and Down (Levodepression): Consistent with the pattern so far, looking left and down is simply a matter of using the opposite EOM when looking right and down: right SO and left IR (see figure 8). This is due to the right eye being adducted (depressed by the SO when toward the nose) and the left eye being abducted (depressed by the IR when away from the nose).
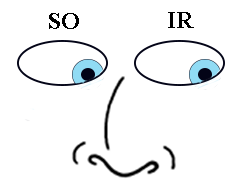
FIGURE 8.
» Looking Straight Down (Infraversion): Downward gaze also involves two muscles, but this time the LR and MR are not involved. Instead, both downward rotating muscles are engaged simultaneously: the right IR and SO, and the left IR and SO. The mechanics behind this (greatly simplified) relate to the different angles of attachment of the IR and SO; this is also the reason behind the IR and SO being restricted to depressing the eye during adbuction and adduction, respectively. When the IR and SO contract simultaneously, the toward-the-nose and away-from-the-nose forces cause the eye to rotate straight down (see figure 9).

FIGURE 9.
» Looking Straight Up (Supraversion): This pair of yoked muscles offers no surprises: looking straight up uses the same principles as looking straight down, but with the opposite muscles: the right SR and IO, and the left IO and SR (see figure 10).

FIGURE 10.
» Crossing the Eyes (Convergence): Convergence occurs when the left and right MR muscles are contracted simultaneously, rotating both eyes horizontally toward the nose (see figure 11). This is more than a way to view certain 3D images - the eyes converge as an object of focus moves closer to the viewer. The opposite, divergence, is not listed here because one cannot (voluntarily) contract both LR muscles simultaneously.

FIGURE 11.
You are now familiar with the 6 cardinal directions of gaze (right/up; right; right/down; left/up; left; left/down), as well as the remainder of the yoked eye movements (straight up; straight down; convergence). Click on the following link for a great interactive eye simulator to practice what you know. You can lesion muscles and/or cranial nerves (covered later on this site) and even take a quiz to isolate lesions. Some of the quiz questions involve cranial nerves, so you may want to read through that section on this site before taking the quiz.


Laws of Eye Movements1 2 3
We will now briefly discuss several laws governing the movements of the eyes. These laws will help to clarify the limitations and boundaries of the extra-ocular muscles and permittable orientations of the eyes in their bony orbits.
Hering's Law
Hering's Law states that yoked muscles receive the same amount of innervation, and at the same time. This may seem painfully simple, but this is an important principle which underscores the connection between muscles and movements that are considered "yoked". In fact, this priniciple partly explains why both eyes are effected during pathologic nystagmus. An example of this law would be the equal and simultaneous innervation of the left LR and right MR when looking to the left. Hering's Law is the essence of what makes these movements yoked.
Sherrington's Law
Sherrington's Law explains that any increase in innervation to an agonist muscle must also include a simultaneous decrease in innervation to the antagonist muscle. Let's define these two terms to understand this law more fully.
- Agonist Muscle
- A muscle that on contracting is automatically checked and controlled by the opposing simultaneous contraction of another muscle—called also agonist muscle, prime mover. 4
- Antagonist Muscle
- An agent that acts in physiological opposition: a muscle that contracts with and limits the action of an agonist with which it is paired—called also antagonistic muscle. 4
The short version of these formal definitions can be reworded as an agonist muscle being the muscle that works to achieve a desired action (e.g. looking left), while an antagonist muscle exists to perform the opposite action (e.g. looking right). What is important to keep in mind is that these labels are relative: for example, if the desired action is to look right, the muscles involved become the agonist muscles and the those responsible for looking left become the antagonist.
Sherrington's Law is quite reasonable then: an increase in innveration to the agonist muscle (making a desired movement) must be accompanied by an equal decrease in innervation to that muscle's antagonist (the muscle that would do the opposite). This law nicely illustrates the relationship between paired agonist/antagonist extraocular muscles. A diagram may help to solidify this point (see figure 12 below).

FIGURE 12. Agonst/antagonist EOM when looking left and right.
From figure 12 you can easily see that the LR and MR are paired agonist/antagonist muscles. When one contracts, the other must relax, otherwise the muscles would be fighting aginst each other and the eye would remain motionless. The six EOM can be grouped into three pairs of agonist/antagonist muscles when considering just one eye:
- Agonist/Antagonist Pairs in the Same Eye
- Lateral Rectus vs. Medial Rectus
- Superior Rectus vs. Inferior Rectus
- Superior Oblique vs. Inferior Oblique
We have already seen the pairings (albeit without the agonist/antagonist terminology) when considering both eyes in our discussion of the cardinal directions of gaze (figures 3 - 10). The table below summarizes the agonist pairs when considering both eyes, for your reference:
TABLE 1. The paired agonist muscles across both eyes.| Right Eye | Left Eye | Movement |
|---|---|---|
| Lateral Rectus | Medial Rectus | Move the globe to the right |
| Medial Rectus | Lateral Rectus | Move the globe to the left |
| Superior Rectus | Inferior Oblique | Move the globe upward |
| Inferior Oblique | Superior Rectus | Move the globe upward |
| Superior Oblique | Inferior Rectus | Move the globe downward |
| Inferior Rectus | Superior Oblique | Move the globe downward |
Donders' Law
Before we discuss the next two laws (Donders' and Listing's) you should be aware of a fantastic, free tutorial of eye movements from the University of Western Ontario. It covers the next two laws, as well as immediately related topics in depth, in an interactive manner. It's really worth visiting.
Donders' Law deals with the position of the eye in the orbit when looking in a particular direction. Before we can delve any further, however, we need a little background information.
The EOM have the ability to move the globe of the eye in 3 dimensions. Those directions are:
- 3D Eye Movements
- Yaw (side-to-side)
- Pitch (front-back)
- Roll (clockwise-counterclockwise)
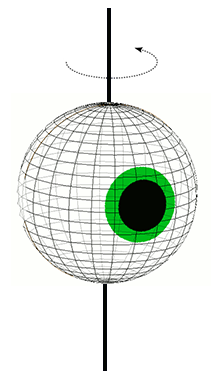
FIGURE 13. Eye rotation in the yaw (side-to-side) plane.
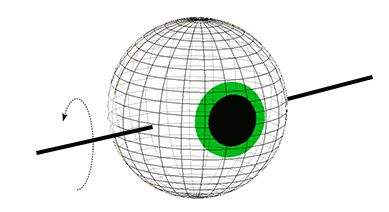
FIGURE 14. Eye rotation in the pitch (front-back) plane.

FIGURE 15. Eye rotation in the roll (clockwise-counterclockwise) plane.
The EOM can focus an object on the fovea (for optimal vision) using only vertical and horizontal movements (2 dimensions). Because of the degree of freedom provided by the roll plane (the 3rd dimension), there are a number of possible degrees of orientation the eyes can assume along the roll plane with the same visual results (i.e. object focused on the fovea). For example, after the horizontal and vertical movements focus an image on the fovea, in terms of visual acuity, the globe technically has the freedom to rotate 1, 2, 3, 4.... degrees in the roll plane to the right or left without affecting vision. But Donders' Law states that despite these several possible orientations, the globe always assumes the same position (even in the roll plane) while looking in a given direction. Therefore Donders' Law is not a mechanical constraint, but a neural one. Thus regardless of which series of movements the eye makes in order to look, for example, down and right, from whatever previous position, the orientation of the globe in the bony orbit for "down and right" is always the same.
Listing's Law
Listing's Law is like a more specific Donders' Law: it accepts the eye has the same 3 dimensional orientation for looking in a given direction (Donders' Law), and more specifically provides a rational for what that unique orientation is. Listing found that the required axes to make the globe move in the cardinal directions of gaze and follow Donders' Law were all in the same plane. Figure 16 below shows what is called Listing's Plane:
Note all the axes are in the plane of the blue box (the plane of your computer screen). This has important implications about the effort required in holding eccentric gaze (it is reduced) and a host of other factors. Going further into this requires an explanation of rotational kinematics, which is outside the scope of this website. Suffice it to say that there are options for movements that the eyes could make, but do not. The interplay between the effort in holding steady gaze, counteracting muscle elasticity and viscosity are worth researching on your own, but are not covered here.
A final word on Listing's Law and Plane. There are, of course, exceptions to these rules. As you may have noticed, Listing's Plane is 2 dimensional. Any eye movements that rotate around an axis protruding from the plane would violate the law. Refer to figure 15 above to review the roll plane; that axis (the 3rd dimension) would violate Listing's Law. And we, of course, make use of torsional eye movements all the time. One paramount example for balance clinicians is the VOR in the roll plane. Move your head from shoulder to shoulder (roll) and this screen/text remains in the same orientation. This is because your eyes are rotating in the opposite direction of head movement (i.e., the VOR) to maintain stability of the image in front of you. Since this is done in the roll plane, which violates Listing's Law, the roll plane VOR is an important example of an exception to Listing's Law.


- Page References - Click the links below for full citations
- Theory of Eye Motion and Neurological Testing
- The Extraocular Muscles
- Basic Clinical Neuroscience (Third Edition)
- MedlinePlus Medical Dictionary




